As the old saying goes: “In theory, there is no difference between theory and practice — but in practice, there is.”
This tension has shown up in theoretical computer science in recent years as researchers increasingly try to tackle difficult algorithmic problems by borrowing from the field of deep learning and neural networks, which often perform well without us knowing why.
“Theoretical approaches analyze how good procedures are, but are often designed with the worst case in mind, and may not be the best for all the problems that you actually see in practice,” says MIT professor Stefanie Jegelka, who does research in machine learning at the Computer Science and Artificial Intelligence Lab (CSAIL). “On the other hand, we have these learned methods that might work in practice, but we don't know exactly when or why, so there are no theoretical guarantees.”
Jegelka’s intention in recent work is to build theoretical foundations showing that certain types of neural networks can perform optimally, with reliable guarantees for approximately how accurate their results will be. Her team has specifically explored whether “graph neural network” (GNN) architectures can be designed to capture optimal approximation algorithms for a wide range of problems, including “NP-hard problems” that require optimizing a function over discrete inputs.
Traditional approaches to combinatorial optimization often involve a trade-off between efficiency and optimality. But in a new paper Jegelka and her team at MIT’s Computer Science and Artificial Intelligence Lab (CSAIL) show that polynomial-sized message-passing algorithms—which GNNs can represent—can achieve optimal approximation ratios for a range of so-called max-constraint satisfaction problems (Max-CSPs), like maximum-cut, minimum vertex cover, and, yes, even Sudoku.
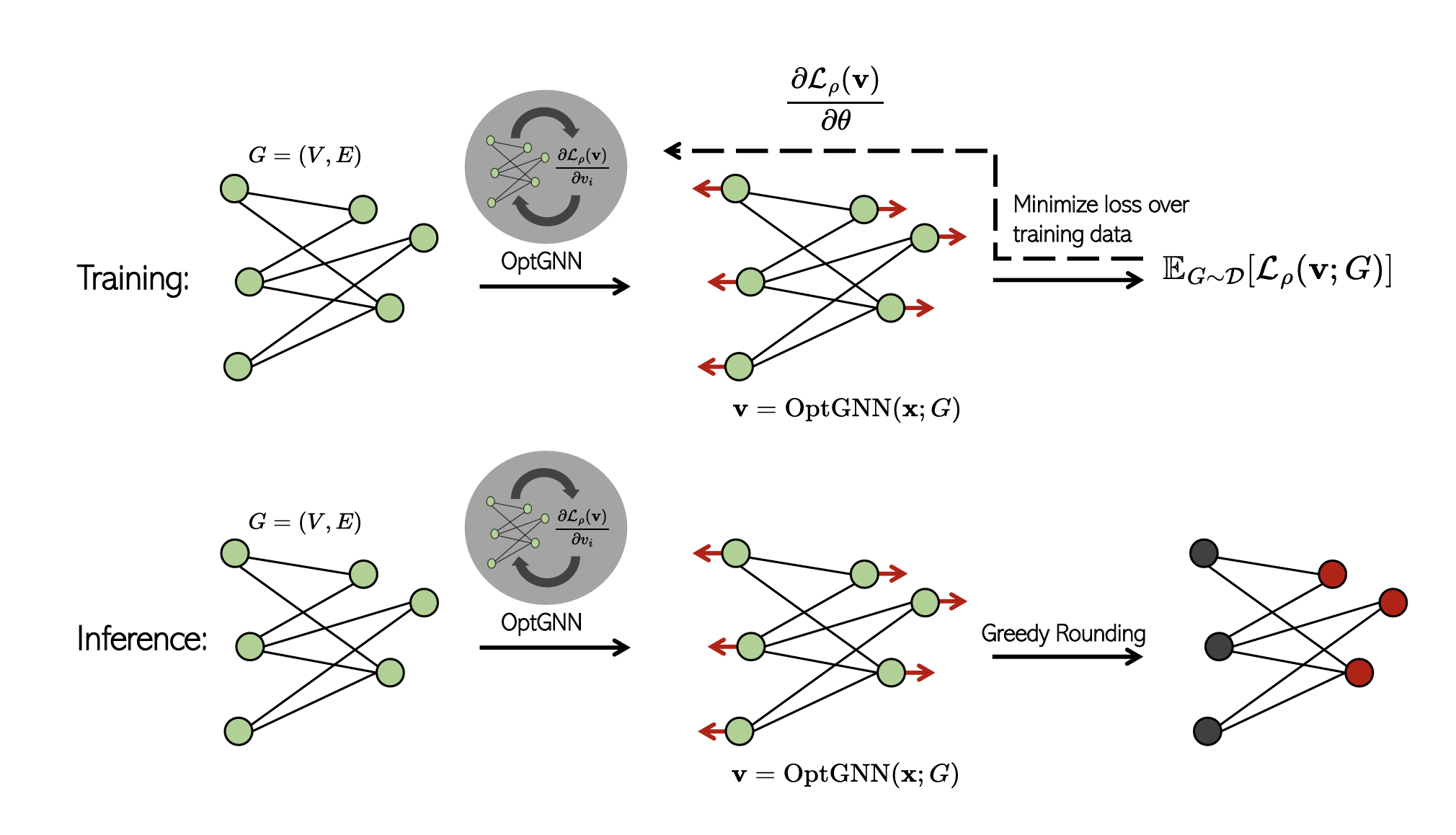
Leveraging tools from semidefinite programming (SDP), a technique known for providing strong approximation guarantees for many NP-hard problems, the researchers developed an architecture they call “OptGNN,” which they show to be simple to implement and capable of competitive results across various real-world and synthetic datasets for a range of Max-CSPs, as compared to classical heuristics, solvers and state-of-the-art neural baselines.
“OptGNN achieves the appealing combination of obtaining approximation guarantees while also being able to adapt to the data to achieve improved results,” says PhD student Morris Yau, lead author on the new paper about the project, which will be a spotlight presentation at the Conference on Neural Information Processing Systems (NeurIPS) next month in Vancouver.
Jegelka and Yau both see a lot of benefits for neural networks that draw from theoretical models.
“Not every algorithm is optimal for every problem, so one advantage with an approach that is learnable is that it can adapt to the data at hand. If you train it on enough examples, it will be more specialized,” Jegelka says.
One challenge that arose in the team’s work was how to handle the inherent discreteness of combinatorial optimization problems. SDP techniques typically produce vector-valued solutions to discrete problems in a “lifted space” - OptGNN, meanwhile, produces vector-valued solutions as its initial output, but then rounds them to feasible integral solutions using a randomized rounding technique.
A key advantage to OptGNN is that its generalized architecture can adapt to different problems, with users only needing to provide the appropriate Lagrangian for their specific problem. The message-passing updates are then handled automatically through automatic differentiation.
“It's essentially a more plug-and-play approach to neural combinatorial optimization,” says Jegelka. “This simplifies the process significantly compared to designing and implementing task-specific neural architectures.”
There are some observable limitations to the scope of the current study. For one, the theoretical guarantees rely on the Unique Games Conjecture, which remains unproven. Also, the sample complexity analysis provides some insight, but doesn't fully explain the empirical success of deep networks in general. Yau says that further research is needed to improve rounding procedures and develop more robust neural certification schemes.
Looking ahead, the team says that OptGNN opens up several directions for future exploration, such as the design of powerful rounding procedures that can secure approximation guarantees, the construction of state-of-the-art neural certificates, and the design of neural SDP-based branch and bound solvers. While the paper does show that OptGNN is capable of achieving the approximation guarantee efficiently, it still remains to be seen if researchers can show that a neural network can secure the guarantee in all practical instances.
Co-author and CSAIL postdoctoral fellow Nikolaos Karalias says that the tool could help reduce the burden on researchers in their work on difficult algorithmic problems.
“You usually need some kind of human expertise to crack the problem, but the ultimate goal with neural-net-based solvers is to automatically adapt to the problem at hand, while producing solutions of certified quality - all without a human in the middle,” says Karalias.
Yau, Jegelka and Karalias co-authored the paper with PhD student Eric Lu from Harvard University, and independent researcher Jessica Xu. The work was funded in part by the National Science Foundation and the Swiss National Science Foundation.





